Seputar Pengetahuan: Luas Permukaan Kubus, Balok, Tabung, Prisma Segi Empat, Prisma, Kerucut, dan Volumenya

Luas Permukaan Kubus

1. Luas Permukaan Kubus

Kubus ABCD.EFGH dengan panjang rusuk s satuan

Luas BCGF   = s x s
                    = s²
Luas Permukaan Kubus ABCD.EFGH
                    = 6 x Luas BCGF
                    = 6.s²

Luas Permukaan Kubus dengan panjang sisi s satuan adalah 6.s² satuan luas

2. Contoh Soal

1. Hitung Luas permukaan kubus dengan panjang rusuk 7 cm !

Jawab :
Luas permukaan kubus = 6 x s²
    = 6 x 72
    = 6 x 49
    = 294 cm²

2. Hitung Luas permukaan kubus jika luas salah satu sisinya 10 cm² !

Jawab :
Luas salah satu sisi   = 10
                           s² = 10
Luas permukaan kubus = 6 x s²
                                      = 6 x 10²
                                      = 6 x 100
                                      = 600 cm²

3. Luas permukaan kubus adalah 600 cm². Hitung panjang rusuk kubus tersebut !

Jawab :

Luas permukaan kubus = 6 x s² 600 = 6 x s²
s² =

s² = 100
s = 10 cm

Volum Kubus

1. Volum Kubus

Kubus ABCD dengan panjang rusuk s satuan

Luas Alas ABCD  = sisi x sisi
                             = s x s
                             = s²
Volum Kubus       = Luas Alas ABCD x tinggi
                          = s²                       x s
                          = s³

Volum Kubus dengan panjang sisi s satuan adalah s³ satuan volum.

2. Contoh Soal

1. Hitung Volum kubus yang mempunyai rusuk 9 cm !

Jawab :

Volum   = s³
            = 9³
            = 729 cm³.

2. Hitung Volum kubus jika luas salah satu sisinya 9 cm² !

Jawab :

Luas salah satu sisi = 9
s² = 9
s = 3 cm

Volum = s³
= 3³
= 27 cm³

3. Volum sebuah kubus adalah 125 cm³. Hitung panjang rusuk kubus tersebut !

Jawab :

Volum = s³

125 = s³

5³ = s³
s = 5 cm

Luas Permukaan Balok

Perhatikan gambar balok !

Luas ABCD = AB x BC = p x l
Luas ABFE = AB x BF = p x t
Luas ADHE = AD x AE = l x t
Luas Permukaan balok ABCD.EFGH = 2 Luas ABCD + 2 Luas ABFE + 2 Luas ADHE
= 2 pl + 2 pt + 2 lt

CONTOH SOAL :

1. Hitung Luas permukaan balok dengan ukuran 2 cm x 3 cm x 4 cm !

Jawaban :

2. Hitung Luas permukaan balok jika alasnya persegi dengan panjang sisi 4 cm dan tinggi balok
5 cm !

Jawaban :

3. Luas permukaan balok adalah 108 cm². Hitung tinggi balok jika panjangnya 4 cm dan lebarnya
3 cm !

Jawaban :

Volume Balok

Perhatikan balok ABCD.EFGH !

Luas Alas ABCD = AB x BC
= p x l
= pl

Volum balok = Luas Alas ABCD x tinggi
= pl x t

CONTOH SOAL :

1. Hitung Volum balok dengan ukuran 6 cm x 5 cm x 4 cm !

Jawaban :

2. Hitung tinggi balok jika diketahui Volum balok 200 cm, panjang 5 cm dan lebar 4 cm !

Jawaban :

3. Volum sebuah balok adalah 250 cm³. Jika alasnya berbentuk persegi dan tinggi balok 10 cm,
hitung panjang rusuk alas !

Jawaban :

Luas Permukaan Tabung

Untuk mencari luas permukaan tabung dapat menggunakan jaring-jaring tabung. Jaring-jaring tersebut terdiri dari :

Selimut tabung yang berupa persegi panjang dengan panjang = keliling alas tabung = 2πr dan lebar = tinggi tabung = t, Luas = 2πrt.Dua buah lingkaran (alas dan tutup) berjari-jari r. Luas =2πr² Dengan demikian, luas selimut tabung dapat ditentukan dengan cara berikut :
Luas selimut tabung = keliling alas (p) x tinggi tabung (l)
= 2πr x t
= 2πrt
Luas alas dan tutup tabung = πr² + πr² = 2πr²
Luas permukaan tabung =Luas alas + tutup + luas selimut tabung

Luas permukaan tabung = 2πr²+2πrt = 2πr(r+t)

Contoh soal :
Sebuah tabung memiliki tinggi 25 cm dan jari-jari alas tabung 14 cm, tentukan luas permukaan tabung !
Pembahasan :
Diketahui tinggi tabung 25 cm dan jari-jari alas tabung 14 cm
Luas permukaan tabung = 2πr(r+t)

Luas = 2 x	22	x 14 (14 +25) = 88 x 14 x 39 = 3.342 cm²
	7

Volume Tabung

Rumus volume tabung sama dengan luas alas dikalikan tinggi. Karena tabung memiliki alas berupa lingkaran maka volume tabung sama dengan luas alas lingkaran dikalikan tinggi. Sehingga rumus volume tabung adalah sebagai berikut :

Volume Tabung = πr²t

Contoh soal :
Diketahui tabung dengan jari-jari 7 cm dan tingginya 30 cm.Tentukan volume tabung !
Jawab:
Diketahui tinggi = 20 cm dan jari-jari tabung = 7 cm
Volume tabung = πr²t

Volume =	22	x 7 x 7 x 20 = 22 x 7 x 20 = 154 x 20 = 3.080 cm³
	7

Perhatikan limas T.PQRS berikut ini.

Diketahui limas T.PQRS adalah limas persegi. Jika panjang PQ = 10 cm. Dan tingginya 12 cm, maka berapakah luas permukaan limas tersebut?

Jawab:
LP = Luas alas + luas semua sisi tegak

LP = Luas PQRS + 4 Luas TQR (ingat, limasnya persegi jadi luas sisi tegaknya juga sama)

LP = (10 x 10) + 4 Luas TQR

Nah, untuk mengetahui luas segitiga TQR, kita perlu mencari tinggi segitiga karena alas segitiga sudah diketahui, yaitu 10 cm.

Mencari Panjang TB.

Perhatikan PQ dan OB. OB panjangnya adalah setengan PQ, jadi untuk mencari TB, gunakan phythagoras. TB = akar (OB kuadrat + OT kuadrat)

TB = akar (25 + 144)

TB = akar 169

TB = 13 cm

Mencari luas 4 sisi tegak.

Karena sisi tegak berbentuk segitiga, maka luasnya adalah:

Luas permukaan limas = 10 x 10 + 260

Luas permukaan limas = 100 + 260

Luas permukaan limas = 360 cm^2

Begitulah cara menghitung limas segiempat. Coba cari soal-soal mengenai luas permukaan limas yang alasnya tidak berbentuk persegi.

Luas Permukaan Prisma

Luas permukaan prisma dapat ditentukan dengan menjumlahkan luas sisi-sisi tegak, luas alas dan luas bidang atas.

Misal : Prisma segitiga ABC.EFG

Jika diiris menurut rusuk-rusuk FC, DF, EF, AC dan BC maka didapat jaring-jaring ;

Luas permukaan prisma = ( luas EDF + luas ABC) + (luas ACFD + luas CBEF + luas BADE)
                                    = ( 2 x luas ABC ) + { ( AC x t ) + ( CB x t ) + ( BA x t ) }
                                     = ( 2 x luas alas ) + { t ( AC + CB + BA ) }
                                     = ( 2 x luas alas ) + ( t x keliling alas )
Kesimpulan :

Luas permukaan prisma = ( 2 x luas alas ) + ( keliling alas x tinggi )

Contoh :

Hitunglah luas permukaan prisma segitigadengan alas berbentuk segitiga siku-siku berukuran 3cm, 4cm, 5cm dan tinggi prisma 10 cm !

Jawab:

Sisi alas; a = 3 cm
                t = 4 cm

Luas alas     =

                   =

= 6 cm²

Keliling alas = 3 cm + 4 cm + 5 cm
= 12 cm

Luas permukaan prisma = ( 2 x luas alas ) + ( keliling alas x tinggi )
                                      = (2 x 6 cm² ) + ( 12 cm x 10 cm )
                                      = 12 cm² + 120 cm²
                                       = 132 cm²

Jadi luas permukaan prisma 132 cm²

Volume Prisma

Volum limas dapat ditentukan dengan membelah sebuah balok menjadi dua bagian sama besar melalui salah satu diagonal bidang sehingga membentuk dua prisma yang kongruen.

2 Volum prisma =  volume balok
                           =   p x l x t

Volum prisma      =

x p x l x t

Volum prisma = (

xluas alas balok) x t

Volum prisma = luas alas prisma x t
Volum prisma = luas alas x tinggi

Kesimpulan :

Volum Prisma = luas alas x tinggi

Contoh :
Hitunglah volum prisma segilima jika luas alasnya 50 cm² dan tinggi 15 cm !

Jawab :
Luas alas = 50 cm²

t = 15 cm

Volum prisma = luas alas x tinggi
                      = 50 cm² x 15 cm
                      = 750 cm³

Jadi volum prisma segilima 750 cm³

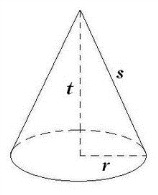
Luas Permukaan Kerucut dan Volume

Di bawah ini merupakan gambar atau struktur dari sebuah kerucut.

Dan jika gambar tersebut dipisahkan dalam beberapa bagian maka akan nampak seperti gambar di bawah ini.

Setelah kita mengetahui gambar dari kerucut maka kita pun dapat menentukan rumus untuk mencari volume dan luas permukaan dari sebuah bangunan berbentuk kerucut.

Rumus Kerucut

Luas alas